Newtonian Physics¶
Introduction: Why Tensors¶
This section gives a brief introduction, and in the next sections we derive everything in detail. The Newton law is:
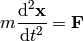
and using a potential for 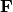 , we get:
, we get:
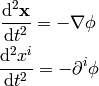
the last two equations are two different equivalent ways to write a tensor
equation in 3D, which means that this equation has the exact same form (is
valid) in any (spatial) coordinate system (rotated, translated, in cartesian
coordinates, spherical coordinates, ...). Each coordinate system has a
different metric, but we can always locally transform into
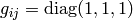 .
.
However, if our coordinate transformation depends on time (e.g. a rotating disk), then the above tensor equation changes (e.g. for the rotating disk, we get the Coriolis acceleration term), that’s because time is treated as a parameter, not as a coordinate.
To fix this, we need to work in 4D and treat time as a coordinate, so we
introduce 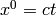 where
where  is any constant speed (it can be any speed,
doesn’t have to be the speed of light). Then in 4D, the above equations are not
tensor equations anymore, because the operator
is any constant speed (it can be any speed,
doesn’t have to be the speed of light). Then in 4D, the above equations are not
tensor equations anymore, because the operator 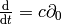 is not a tensor. The 4D tensor formulation happens to be the geodesic equation:
is not a tensor. The 4D tensor formulation happens to be the geodesic equation:
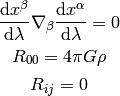
Which (given that we know how to calculate the Ricci tensor in our coordinates) is valid in any coordinates, not only rotated, translated, cartesian, spherical, ..., but also with arbitrary time dependence, e.g. a rotating disk, accelerating disk, ...
After suitable local coordinate transformation, we can only get two possible
metrics (that connect the time and spatial coordinates): 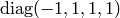 and
and 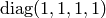 . Inertial systems have no fictitious forces, so the
metrics is one of the two above (possibly with
. Inertial systems have no fictitious forces, so the
metrics is one of the two above (possibly with  ). Transformation
between inertial systems is such a coordinate transformation that leaves the
metric intact, e.g.:
). Transformation
between inertial systems is such a coordinate transformation that leaves the
metric intact, e.g.:
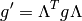
There is no coordinate transformation that turns the metric 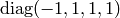 into
into 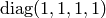 , so we need to choose either one to describe one
inertial system and then all other inertial systems will automatically have a
metric with the same signature.
, so we need to choose either one to describe one
inertial system and then all other inertial systems will automatically have a
metric with the same signature.
The Newton law is valid for small speeds compared to the speed of light, so
when we want to extend the theory for all speeds, we only have 4 options: O(3,
1) with either 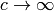 or
or  finite and O(4) with either
finite and O(4) with either 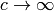 or
or
 finite. If
finite. If  is finite, it has to be large enough, so that we still
recover the Newton law for small speeds with the given experimental precision.
All 4 cases give the correct Newton law, but give different predictions for
large speeds. All we need to do to decide which one is correct is to perform
such large speeds (relativistic) experiments. It turns out that all such
relativistic experiments are in agreement with the O(3, 1) case where
is finite, it has to be large enough, so that we still
recover the Newton law for small speeds with the given experimental precision.
All 4 cases give the correct Newton law, but give different predictions for
large speeds. All we need to do to decide which one is correct is to perform
such large speeds (relativistic) experiments. It turns out that all such
relativistic experiments are in agreement with the O(3, 1) case where  is
the (finite) speed of light and with disagreement with the 3 other cases. For
small speeds however (i.e. Newtonean physics), all 4 cases will work, as long
as
is
the (finite) speed of light and with disagreement with the 3 other cases. For
small speeds however (i.e. Newtonean physics), all 4 cases will work, as long
as  is chosen large enough.
is chosen large enough.
Given a tensor equation, we can easily determine, if it transforms correctly
under the Galilean (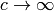 ) or Lorentz transformations (
) or Lorentz transformations ( is finite).
All we have to do is to perform the limit
is finite).
All we have to do is to perform the limit 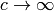 . For example the Newton
second law is recovered if we do the
. For example the Newton
second law is recovered if we do the 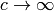 limit, but Maxwell equations
are only recovered if we choose
limit, but Maxwell equations
are only recovered if we choose  to be exactly the speed of light in the
Maxwell equations.
to be exactly the speed of light in the
Maxwell equations.
The reason why we write equations as tensor equations in 4D is that we can then use any coordinates (including any time dependence), i.e. any observer, and the equations still have the exact same form. So specifying the metrics is enough to define the coordinates (observer) and since the equations has only one form, that is all we need. If we write equations only as tensors in 3D, we not only need to specify the (3D) metrics, but also how the observer accelerates with respect to some (usually inertial) frame where the equations (let’s say Newton law) is defined and we then need to transform all the time derivatives correctly. By using tensors in 4D, all those transformations are taken care of by the standard tensor machinery and all we need to care about is exactly one observer, defined by its metric tensor.
By choosing the correct metrics and  (i.e.
(i.e. 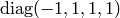 and
and  the
speed of light), all equations are then automatically Lorentz invariant. If we
choose
the
speed of light), all equations are then automatically Lorentz invariant. If we
choose 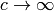 (and any metric), we automatically get all equations
Galilean invariant.
(and any metric), we automatically get all equations
Galilean invariant.
High School Formulation¶
The usual (high school) formulation is the second Newton’s law:
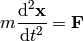
for some particle of the mass 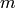 and position
and position 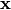 . To determine the
force
. To determine the
force 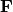 , we have at hand the Newton’s law of
gravitation:
, we have at hand the Newton’s law of
gravitation:
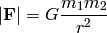
that expresses the magnitude  of the force between two particles with
masses
of the force between two particles with
masses 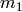 and
and 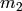 and we also know that the direction of the force is
directly towards the other particle.
We need to take into account all particles in the system, determine the
direction and magnitude of the force due to each of them and sum it up.
and we also know that the direction of the force is
directly towards the other particle.
We need to take into account all particles in the system, determine the
direction and magnitude of the force due to each of them and sum it up.
College Formulation¶
Unfortunately, it is quite messy to keep track of the direction of the forces
and all the masses involved, it quickly becomes cumbersome for more than 2
particles. For this reason, the better approach is to calculate the force
(field) from the mass density function  :
:
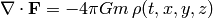
To see that both formulations are equivalent, integrate both sides inside some sphere:
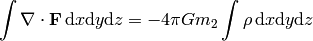
apply the Gauss theorem to the left hand side:
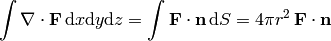
where 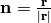 and
the right hand side is equal to
and
the right hand side is equal to 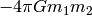 and we get:
and we get:
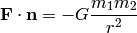
now we multiply both sides with  , use the fact that
, use the fact that
 (because
(because 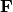 is spherically
symmetric), and we get the traditional Newton’s
law of gravitation:
is spherically
symmetric), and we get the traditional Newton’s
law of gravitation:
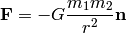
It is useful to deal with a scalar field instead of a vector field (and also
not to have the mass 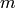 of the test particle in our equations explicitly), so we
define a gravitational potential by:
of the test particle in our equations explicitly), so we
define a gravitational potential by:
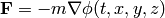
then the law of gravitation is
(1)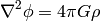
and the second law is:
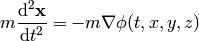
Note about units:
![[r] = [{\bf x}] = \rm m](../../_images/math/22b9c6fec5cb4c0bd4ad12eb6dcd4d733a4dda81.png)
![[m] = \rm kg](../../_images/math/6b8e3dbe5aabd29f1c9d9f1bd66afc77c1c314f2.png)
![[\rho] = \rm kg\,m^{-3}](../../_images/math/b2e89118ff5c0378b0208da95e781215131cc26e.png)
![[F] = \rm kg\,m\,s^{-2}](../../_images/math/d2b95d5bd0c33f3051dea4aa00777a677ecb4575.png)
![[G] = \rm kg^{-1}\,m^3\,s^{-2}](../../_images/math/d566403f7a8e81a616d586a3645866072ddd3c33.png)
![[\phi] = \rm m^2\,s^{-2}](../../_images/math/e76997e56cdb4414b1f199e7323ce4f8ec81731f.png)
Differential Geometry Formulation¶
There are still problems with this formulation, because it is not immediatelly clear how to write those laws in other frames, for example rotating, or accelerating – one needs to employ nontrivial assumptions about the systems, space, relativity principle and it is often a source confusion. Fortunately there is a way out — differential geometry. By reformulating the above laws in the language of the differential geometry, everything will suddenly be very explicit and clear. As an added bonus, because the special and general relativity uses the same language, the real differences between all these three theories will become clear.
We write 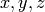 and
and 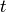 as components of one 4-vector
as components of one 4-vector
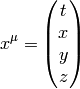
Now we need to connect the Newtonian equations to geometry. To do that, we reformulate the Newton’s second law:
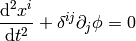
by choosing a parameter 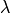 such, that
such, that 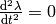 ,
so in general
,
so in general
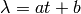
and
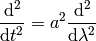
so
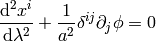
and using the relation 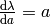 we get
we get
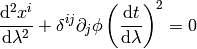
So using 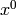 instead of
instead of 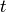 , we endup with the following equations:
, we endup with the following equations:
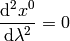
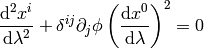
But this is exactly the geodesic equation for the following Christoffel symbols:
(2)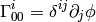
and all other components are zero.
In order to formulate the gravitation law, we now need to express
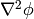 in terms of geometric quantities like
in terms of geometric quantities like
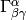 or
or 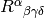 .
We get the only nonzero components of
the Riemann tensor:
.
We get the only nonzero components of
the Riemann tensor:
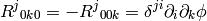
we calculate the 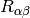 by contracting:
by contracting:
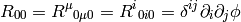
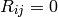
and we see that the Newton gravitation law is
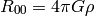
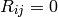
Thus we have reformulated the Newton’s laws in a frame invariant way — the matter curves the geometry using the equations:
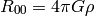
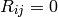
from which one can (for example) calculate the Christoffel symbols and other things. The particles then move on the geodesics:
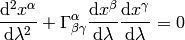
Both equations now have the same form in all coordinate systems (inertial or not) and it is clear how to transform them — only the Christoffel symbols (and Ricci tensor) change and we have a formula for their transformation.
Metrics¶
There is a slight problem with the metrics — it can be proven that there is
no metrics, that generates the Christoffel symbols above. However, it turns out
that if we introduce an invariant speed  in the metrics, then calculate the
Christoffel symbols (thus they depend on
in the metrics, then calculate the
Christoffel symbols (thus they depend on  ) and then do the limit
) and then do the limit
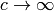 , we can get the Christoffel symbols above.
, we can get the Christoffel symbols above.
In fact, it turns out that there are many such metrics that generate the right
Christoffel symbols. Below we list several similar metrics and the
corresponding Christoffel symbols (in the limit 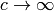 ), so that we can
get a better feeling what metrics work and what don’t and why:
), so that we can
get a better feeling what metrics work and what don’t and why:
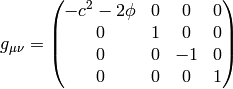
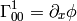
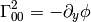
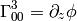
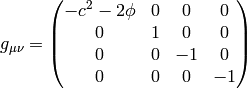
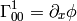
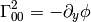
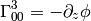
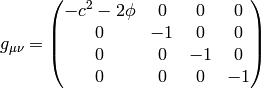
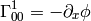
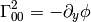
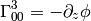
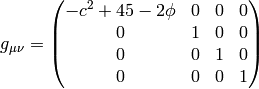
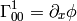
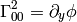
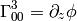
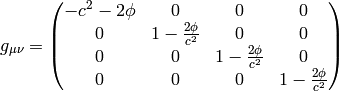
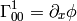
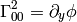
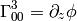
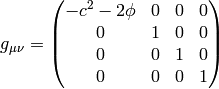
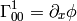
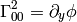
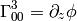
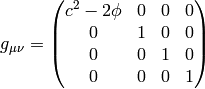
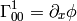
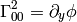
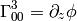
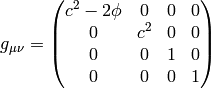
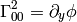
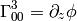
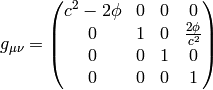
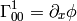
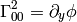
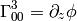
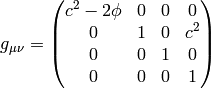
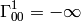
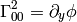
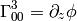
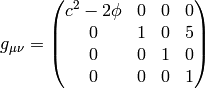
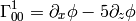
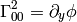
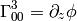
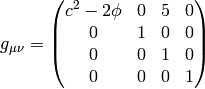
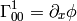
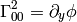
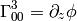
If we do the limit 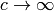 in the metrics itself, all the working metrics
degenerate to:
in the metrics itself, all the working metrics
degenerate to:
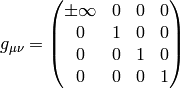
(possibly with nonzero but finite elements 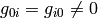 ).
So it seems like any metrics whose limit is
).
So it seems like any metrics whose limit is
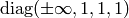 , generates the correct Christoffel symbols:
, generates the correct Christoffel symbols:
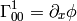
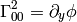
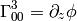
but this would have to be investigated further.
Let’s take the metrics
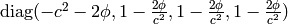 and calculate the Christoffel symbols (without the limit
and calculate the Christoffel symbols (without the limit 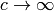 ):
):
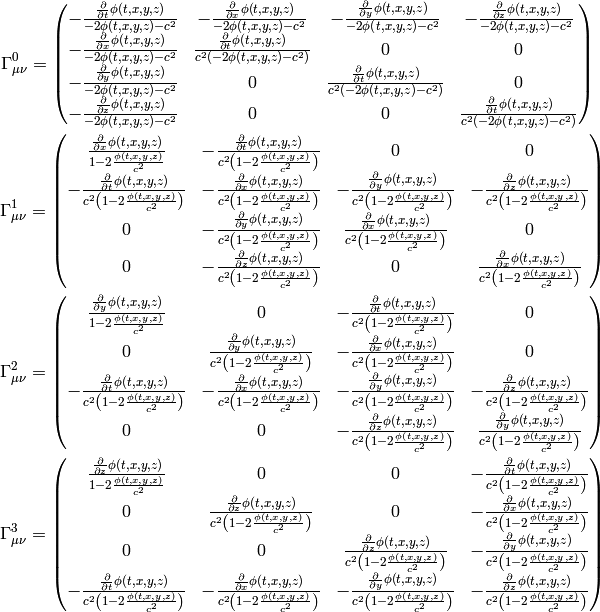
By taking the limit 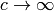 , the only nonzero Christoffel symbols are:
, the only nonzero Christoffel symbols are:
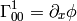
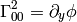
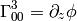
or written compactly:
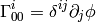
So the geodesics equation
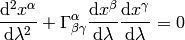
becomes
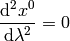
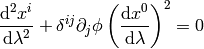
From the first equation we get 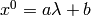 , we substitute to the second
equation:
, we substitute to the second
equation:
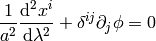
or
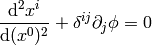
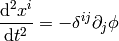
So the Newton’s second law is the equation of geodesics.
Obsolete section¶
This section is obsolete, ideas from it should be polished (sometimes corrected) and put to other sections.
The problem is, that in general, Christoffel symbols have 40 components and
metrics only 10 and in our case, we cannot find such a metrics, that generates
the Christoffel symbols above. In other words, the spacetime that describes
the Newtonian theory is affine, but not a metric space. The metrics is singular,
and we have one metrics 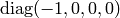 that describes the time coordinate
and another metrics
that describes the time coordinate
and another metrics 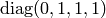 that describes the spatial coordinates.
We know the affine connection coefficients
that describes the spatial coordinates.
We know the affine connection coefficients 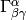 , so
that is enough to calculate geodesics and to differentiate vectors and do
everything we need.
, so
that is enough to calculate geodesics and to differentiate vectors and do
everything we need.
However, for me it is still not satisfactory, because I really want to have a
metrics tensor, so that I can easily derive things in exactly the same way as
in general relativity. To do that, we will have to work in the regime  is
finite and only at the end do the limit
is
finite and only at the end do the limit 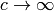 .
.
We start with Einstein equations:
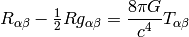
or
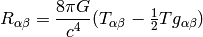
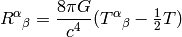
The energy-momentum tensor is
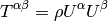
in our approximation 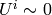 and
and 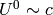 , so the only nonzero component
is:
, so the only nonzero component
is:
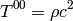
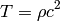
and
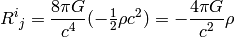
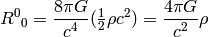
We need to find such a metric tensor, that
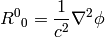
then we get (1).
There are several ways to choose the metrics tensor. We
start
We can always find a coordinate transformation, that converts the metrics to a
diagonal form with only 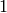 ,
, 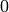 and
and 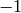 on the diagonal. If we want
nondegenerate metrics, we do not accept
on the diagonal. If we want
nondegenerate metrics, we do not accept 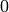 (but as it turns out, the metrics
for the Newtonian mechanics is degenerated).
Also, it is equivalent if we add a minus to all diagonal elements, e.g.
(but as it turns out, the metrics
for the Newtonian mechanics is degenerated).
Also, it is equivalent if we add a minus to all diagonal elements, e.g. 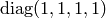 and
and 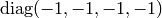 are equivalent, so
we are left
with these options only:
signature 4:
are equivalent, so
we are left
with these options only:
signature 4:
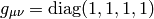
signature 2:
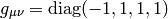
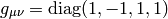
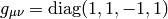
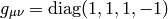
signature 0:
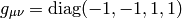
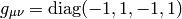
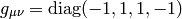
No other possibility exists (up to adding a minus to all elements). We can also
quite easily find coordinate transformations that swap coordinates, i.e. we can
always find a transformation so that we first have only 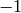 and then only
and then only 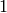 on the diagonal, so we are left with:
signature 4:
on the diagonal, so we are left with:
signature 4:
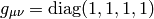
signature 2:
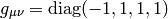
signature 0:
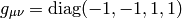
One possible physical interpretation of the signature 0 metrics is
that we have 2 time coordinates and 2 spatial coordinates. In any case, this
metrics doesn’t describe our space (neither Newtonian nor general relativity),
because we really need the spatial coordinates to have the metrics either
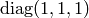 or
or 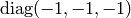 .
.
So we are left with either (this case will probably not work, but I want to have an explicit reason why it doesn’t work):
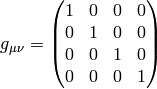
or (this is the usual special relativity)
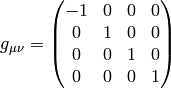
It turns out, that one option to turn on gravitation is to add the term 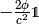 to the
metric tensor, in the first
case:
to the
metric tensor, in the first
case:
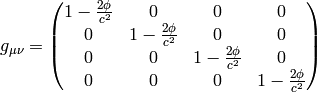
and second case:
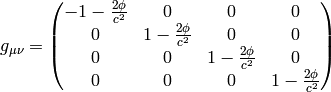
The second law is derived from the equation of geodesic:
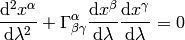
in an equivalent form
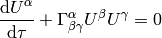
The only nonzero Christoffel symbols in the first case are (in the expressions
for the Christoffel symbols below, we set 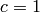 ):
):
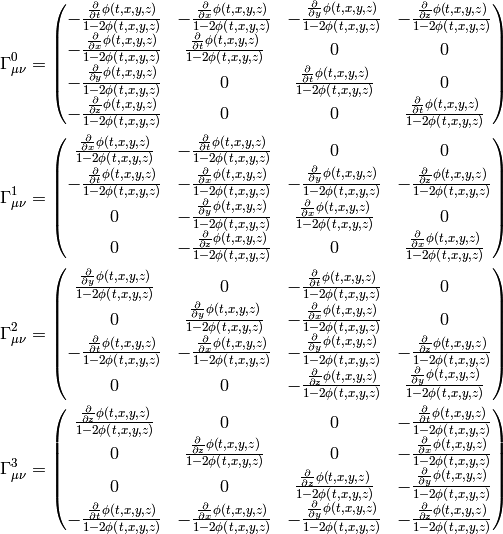
and in the second case, only  is different:
is different:
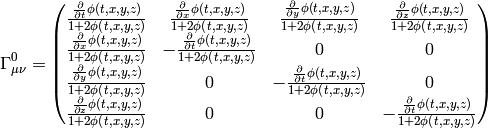
Now we assume that 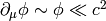 , so all
, so all 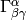 are of the same order. Also
are of the same order. Also 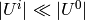 and
and 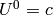 , so the only
nonnegligible term is
, so the only
nonnegligible term is
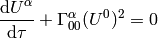
Substituting for the Christoffel symbol we get
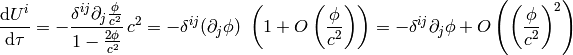
and multiplying both sides with 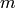 :
:
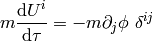
which is the second Newton’s law. For the zeroth component we get (first case metric)
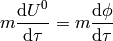
second case:
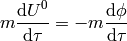
Where 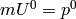 is the energy of the particle (with respect to this frame
only), this means the energy is conserved unless the gravitational field
depends on time.
is the energy of the particle (with respect to this frame
only), this means the energy is conserved unless the gravitational field
depends on time.
To summarize: the Christoffel symbols (2) that we get from the
Newtonian theory contain  , which up to this point can be any speed, for
example we can set
, which up to this point can be any speed, for
example we can set  . However, in order to have some metrics
tensor that generates those Christoffel symbols, the only way to do that is by
the metrics
. However, in order to have some metrics
tensor that generates those Christoffel symbols, the only way to do that is by
the metrics
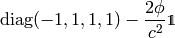
then calculating the Christoffel symbols. If we neglect the terms of the order
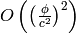 and higher, we get the Newtonian
Christoffel symbols (2) that we want. It’s clear that in order
to neglect the terms, we must have
and higher, we get the Newtonian
Christoffel symbols (2) that we want. It’s clear that in order
to neglect the terms, we must have 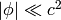 , so we must choose
, so we must choose  large enough for this to work. To put it plainly, unless
large enough for this to work. To put it plainly, unless  is large, there is
no metrics in our Newtonian spacetime. However for
is large, there is
no metrics in our Newtonian spacetime. However for  large, everything is
fine.
large, everything is
fine.
Intertial frames¶
What is an inertial frame? Inertial frame is such a frame that doesn’t have any fictitious forces. What is a fictitious force? If we take covariant time derivative of any vector, then fictitious forces are all the terms with nonzero Christoffel symbols. In other words, nonzero Christoffel symbols mean that by (partially) differentiating with respect to time, we need to add additional terms in order to get a proper vector again – and those terms are called fictitious forces if we are differentiating the velocity vector.
Inertial frame is a frame without fictitious forces, i.e. with all Christoffel symbols zero in the whole frame. This is equivalent to all components of the Riemann tensor being zero:
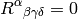
In general, if 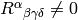 in the whole universe,
then no such frame exists, but one can always achieve that locally, because
one can always find a coordinate transformation so that the Christoffel
symbols are zero locally (e.g. at one point), but unless
in the whole universe,
then no such frame exists, but one can always achieve that locally, because
one can always find a coordinate transformation so that the Christoffel
symbols are zero locally (e.g. at one point), but unless
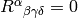 , the Christoffel symbols will not
be zero in the whole frame. So the (local) inertial frame is such a frame that
has zero Christoffel symbols (locally).
, the Christoffel symbols will not
be zero in the whole frame. So the (local) inertial frame is such a frame that
has zero Christoffel symbols (locally).
What is the metrics of the inertial frame? It is such a metrics, that
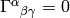 . The derivatives
. The derivatives
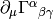 however doesn’t have to be zero. We
know that taking any of the metrics listed above with
however doesn’t have to be zero. We
know that taking any of the metrics listed above with 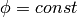 we get all
the Christoffel symbols zero. So for example these two metrics (one with a plus
sign, the other with a minus sign) have all the Christoffel symbols zero:
we get all
the Christoffel symbols zero. So for example these two metrics (one with a plus
sign, the other with a minus sign) have all the Christoffel symbols zero:
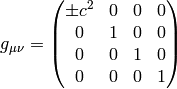
Such a metrics corresponds to an inertial frame then.
What are the (coordinate) transformations, that transform from one
intertial frame to another? Those are all transformations that start with an
inertial frame metrics (an example of such a metrics is given above), transform
it using the transformation matrix and the resulting metrics is also inertial.
In particular, let  be inertial, thus
be inertial, thus  is an inertial
metrics, then transform to
is an inertial
metrics, then transform to 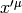 and
and 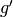 :
:
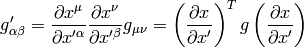
if we denote the transformation matrix by 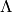 :
:
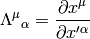
then the transformation law is:
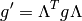
Now let’s assume that 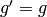 , i.e. both inertial systems are given by the same
matrix and let’s assume this particular form:
, i.e. both inertial systems are given by the same
matrix and let’s assume this particular form:
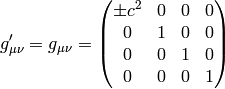
(e.g. this covers almost all possible Newtonian metrics tensors).
Lorentz Group¶
The Lorentz group is O(3,1), e.g. all matrices satisfying:
(3)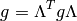
with 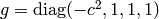 .
Taking the determinant of (3) we get
.
Taking the determinant of (3) we get 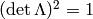 or
or
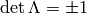 . Writing the 00 component of (3) we get
. Writing the 00 component of (3) we get
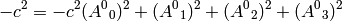
or
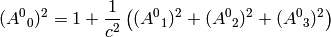
Thus we can see that either 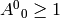 (the transformation preserves the
direction of time, orthochronous) or
(the transformation preserves the
direction of time, orthochronous) or 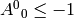 (not orthochronous).
Thus we can see that the O(3, 1) group consists of 4 continuous parts, that
are not connected.
(not orthochronous).
Thus we can see that the O(3, 1) group consists of 4 continuous parts, that
are not connected.
First case: elements with 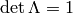 and
and 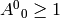 . Transformations
with
. Transformations
with 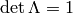 form a subgroup and are called SO(3, 1), if they also have
form a subgroup and are called SO(3, 1), if they also have
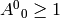 (orthochronous), then they also form a subgroup and are called
the proper Lorentz transformations and denoted by
(orthochronous), then they also form a subgroup and are called
the proper Lorentz transformations and denoted by 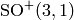 . They
consists of Lorentz boosts, example in the
. They
consists of Lorentz boosts, example in the 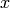 -direction:
-direction:
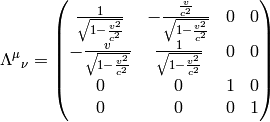
which in the limit 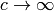 gives
gives
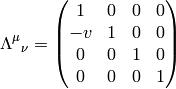
and spatial rotations:
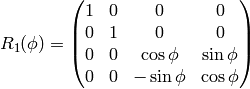
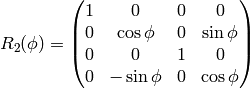
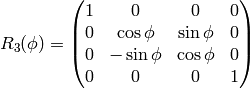
(More rigorous derivation will be given in a moment.)
It can be shown (see below), that all other elements (improper
Lorentz transformations) of the O(3, 1)
group can be written as products of an element from 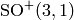 and an
element of the discrete group:
and an
element of the discrete group:
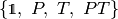
where 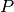 is space inversion (also called space reflection or parity
transformation):
is space inversion (also called space reflection or parity
transformation):
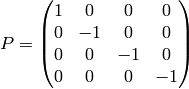
and 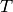 is time reversal (also called time inversion):
is time reversal (also called time inversion):
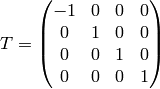
Second case: elements with 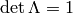 and
and 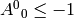 . An example of
such an element is
. An example of
such an element is 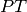 . In general, any product from
. In general, any product from 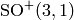 and
and
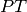 belongs here.
belongs here.
Third case: elements with 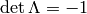 and
and 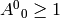 . An example of
such an element is
. An example of
such an element is  . In general, any product from
. In general, any product from  and
and
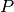 belongs here.
belongs here.
Fourth case: elements with 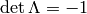 and
and 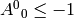 . An example of
such an element is
. An example of
such an element is  . In general, any product from
. In general, any product from 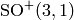 and
and
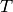 belongs here.
belongs here.
Example: where does the reflection around a
single spatial axis 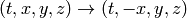 belong to? It is the third
case, because the determinant is
belong to? It is the third
case, because the determinant is 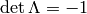 and the 00 element is 1.
Written in the matrix form:
and the 00 element is 1.
Written in the matrix form:
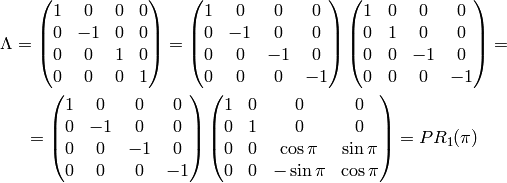
So it is constructed using the 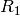 element from
element from 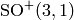 and P
from the discrete group above.
and P
from the discrete group above.
We can now show why the decomposition
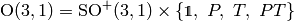 works. Note that
works. Note that
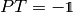 . First we show that
. First we show that 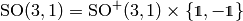 . This follows from the fact, that all matrices with
. This follows from the fact, that all matrices with
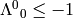 can be written using
can be written using 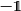 and a matrix with
and a matrix with
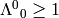 . All matrices
with
. All matrices
with 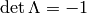 can be constructed from a matrix with
can be constructed from a matrix with 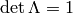 (i.e. SO(3, 1)) and
a diagonal matrix with odd number of -1, below we list all of them together
with their construction using time reversal, parity and spatial rotations:
(i.e. SO(3, 1)) and
a diagonal matrix with odd number of -1, below we list all of them together
with their construction using time reversal, parity and spatial rotations:
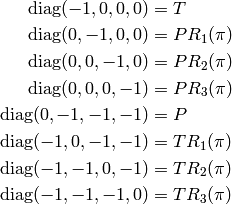
But  belongs to
belongs to 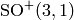 , so we just need two extra
elements,
, so we just need two extra
elements, 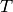 and
and 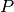 to construct all matrices with
to construct all matrices with 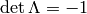 using
matrices from SO(3, 1). So to recapitulate, if we start with
using
matrices from SO(3, 1). So to recapitulate, if we start with 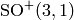 we need to add the element
we need to add the element 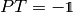 to construct SO(3, 1) and then we need to
add
to construct SO(3, 1) and then we need to
add 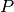 and
and 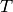 to construct O(3, 1). Because all other combinations like
to construct O(3, 1). Because all other combinations like
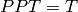 reduce to just one of
reduce to just one of 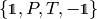 , we are done.
, we are done.
The elements from 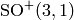 are proper Lorentz transformations, all
other elements are improper. Now we’d like to construct the proper
Lorentz transformation matrix
are proper Lorentz transformations, all
other elements are improper. Now we’d like to construct the proper
Lorentz transformation matrix 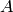 explicitly. As said above, all improper
transformations are just proper transformations multiplied by either
explicitly. As said above, all improper
transformations are just proper transformations multiplied by either 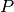 ,
, 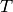 or
or 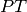 , so it is sufficient to construct
, so it is sufficient to construct 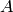 .
.
We can always write 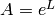 , then:
, then:
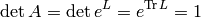
so 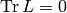 and
and 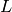 is a real, traceless matrix. Rewriting (3):
is a real, traceless matrix. Rewriting (3):
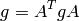
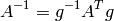
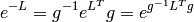
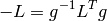
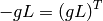
The matrix 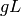 is thus antisymmetric and the general form of
is thus antisymmetric and the general form of 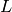 is then:
is then:
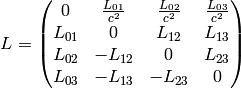
One can check, that 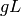 is indeed antisymmetric. However, for a better
parametrization, it’s better to work with a metric
is indeed antisymmetric. However, for a better
parametrization, it’s better to work with a metric 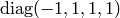 , which
can be achieved by putting
, which
can be achieved by putting  into
into 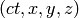 , or equivalently, to work
with
, or equivalently, to work
with 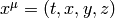 and multiply this by a matrix
and multiply this by a matrix 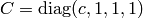 to get
to get 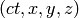 . To get a symmetric
. To get a symmetric 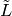 , we just have to do
, we just have to do
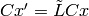 ,
so to get an unsymmetric
,
so to get an unsymmetric 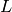 from the symmetric one, we need to do
from the symmetric one, we need to do
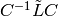 , so we get:
, so we get:
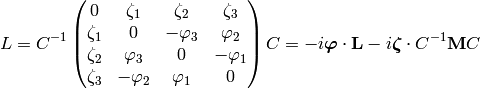
We have parametrized all the proper Lorentz transformations with just 6
parameters
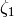 ,
,
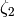 ,
,
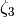 ,
,
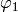 ,
,
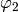 and
and
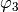 . The matrices
. The matrices 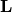 and
and 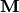 are defined as:
are defined as:
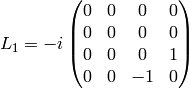
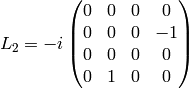
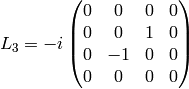
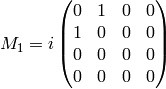
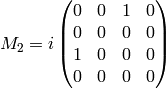
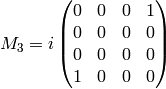
Straightforward calculation shows:
![[L_i, L_j] = i\epsilon_{ijk}L_k](../../_images/math/aaac333280aa89361e3b142a0cabb961dd2ce405.png)
![[L_i, M_j] = i\epsilon_{ijk}M_k](../../_images/math/86d97a1e5ace0e81cb31be4b00400405386ef403.png)
![[M_i, M_j] = -i\epsilon_{ijk}L_k](../../_images/math/de99ee54aa16e84fdab97f8b492ff97161414f7a.png)
The first relation corresponds to the commutation relations for angular
momentum, second relation shows that 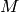 transforms as a vector under rotations
and the final relation shows that boosts do not in general commute.
transforms as a vector under rotations
and the final relation shows that boosts do not in general commute.
We get:
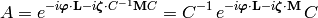
As a special case, the rotation around the  -axis is given by
-axis is given by
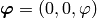 and
and 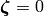 :
:
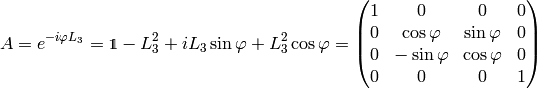
The boost in the  -direction is
-direction is  and
and
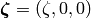 , e.g.:
, e.g.:
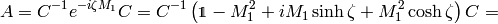
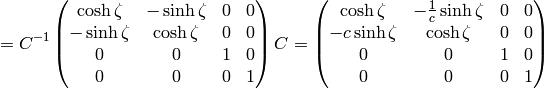
from the construction,  , so we may do the
substitution
, so we may do the
substitution  , where
, where
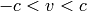 . The inverse transformation is:
. The inverse transformation is:
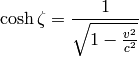
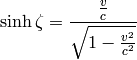
and we get the boost given above:
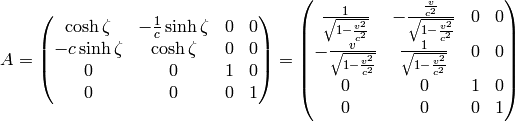
Adding two boosts together:
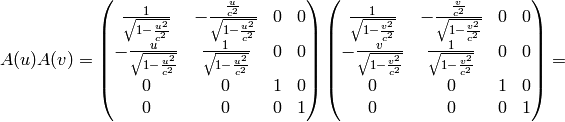
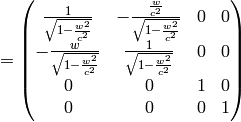
with
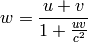
O(4) Group¶
The group of rotations in 4 dimensions is O(4), e.g. all matrices satisfying:
(4)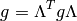
with 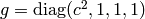 .
Taking the determinant of (4) we get
.
Taking the determinant of (4) we get 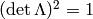 or
or
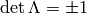 . Writing the 00 component of (4) we get
. Writing the 00 component of (4) we get
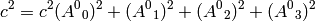
or
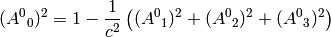
Thus we always have 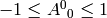 . That is different to the O(3, 1)
group: the O(4) group consists of only 2 continuous parts, that are not
connected. (The SO(4) part contains the element
. That is different to the O(3, 1)
group: the O(4) group consists of only 2 continuous parts, that are not
connected. (The SO(4) part contains the element 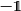 though, but one can get
to it continuously, so the group is doubly connected.)
though, but one can get
to it continuously, so the group is doubly connected.)
Everything proceeds much like for the O(3, 1) group, so 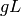 is antisymmetric,
but this time
is antisymmetric,
but this time 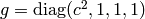 , so we get:
, so we get:
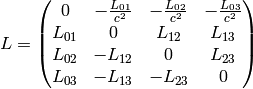
and so we also have 6 generators, but this time all of them are rotations:
with  . The spatial rotations are the same as for O(3, 1)
and the remaining 3 rotations are
. The spatial rotations are the same as for O(3, 1)
and the remaining 3 rotations are 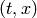 ,
, 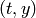 and
and 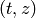 plane rotations.
So for example the
plane rotations.
So for example the 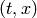 rotation is:
rotation is:
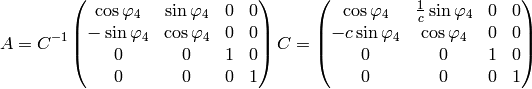
Now we can do this identification:
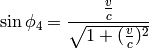
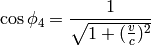
so we get the Galilean transformation in the limit 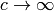 :
:
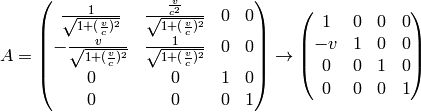
Adding two boosts together:
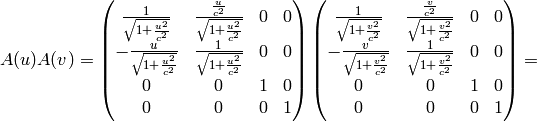
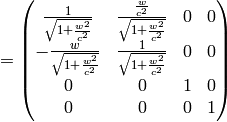
with
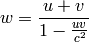
However, there is one peculiar thing here that didn’t exist in the O(3, 1)
case: by adding two velocities less than  , for example
, for example 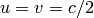 , we get:
, we get:
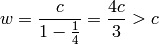
(as opposed to 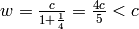 in the O(3, 1) case).
So one can get over
in the O(3, 1) case).
So one can get over  easily. By adding
easily. By adding 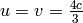 together:
together:
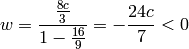
(as opposed to 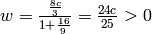 in the
O(3, 1) case). So we can also get to negative speeds easily. One also needs to
be careful with identifying
in the
O(3, 1) case). So we can also get to negative speeds easily. One also needs to
be careful with identifying 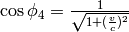 ,
because for
,
because for 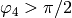 we should probably set
we should probably set 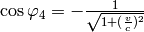 . All of this follows directly from the
structure of SO(4), because one can get from
. All of this follows directly from the
structure of SO(4), because one can get from 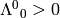 to
to
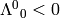 continuously (this corresponds to increasing
continuously (this corresponds to increasing 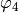 over
over
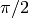 ). In fact, by adding two speeds
). In fact, by adding two speeds 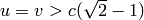 , one always gets
, one always gets
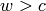 . But if
. But if 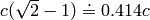 is larger than any speed that we are
concerned about, we are fine.
is larger than any speed that we are
concerned about, we are fine.
Proper Time¶
Proper time 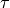 is a time elapsed by (physical) clocks along some (4D)
trajectory. Coordinate time
is a time elapsed by (physical) clocks along some (4D)
trajectory. Coordinate time 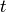 is just some time coordinate assigned to each
point in the space and usually one can find some real clocks, that would
measure such a time (many times they are in the infinity). To find a formula
for a proper time (in terms of the coordinate time), we introduce a local
inertial frame at each point of the trajectory – in this frame, the clocks do
not move, e.g.
is just some time coordinate assigned to each
point in the space and usually one can find some real clocks, that would
measure such a time (many times they are in the infinity). To find a formula
for a proper time (in terms of the coordinate time), we introduce a local
inertial frame at each point of the trajectory – in this frame, the clocks do
not move, e.g. 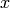 ,
, 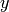 ,
,  is
constant (zero) and there is no gravity (this follows from the definition of
the local inertial frame), so the metric is just a Minkowski metric.
is
constant (zero) and there is no gravity (this follows from the definition of
the local inertial frame), so the metric is just a Minkowski metric.
For any metrics, 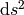 is invariant:
is invariant:
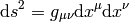
so coming to the local inertial frame, we have  ,
,  ,
,  constant and we
get:
constant and we
get:
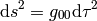
so:
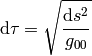
since we are still in the local inertial frame (e.g. no gravity), we have
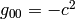 (depending on which metrics we take it could also be
(depending on which metrics we take it could also be 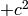 ), so:
), so:
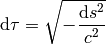
This formula was derived in the local inertial frame, but the right hand side
is the same in any inertial frame, because 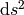 is invariant and
is invariant and  too.
So in any frame we have:
too.
So in any frame we have:
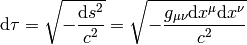
We’ll explain how to calculate the proper time on the 1971 Hafele and Keating experiment. They transported cesium-beam atomic clocks around the Earth on scheduled commercial flights (once flying eastward, once westward) and compared their reading on return to that of a standard clock at rest on the Earth’s surface.
We’ll calculate it with all the metrics discussed above, to see the difference.
Weak Field Metric¶
Let’s start with the metrics:
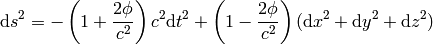
Then:
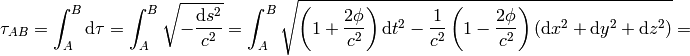
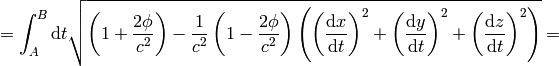
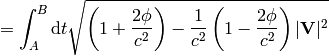
where
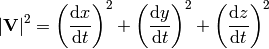
is the nonrelativistic velocity. Then we expand the square root into power
series and only keep terms with low powers of  :
:
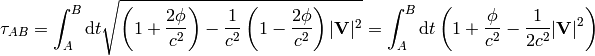
so
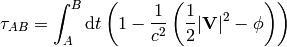
Now let 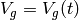 be the speed of the plane relative to the (rotating) Earth
(positive for the eastbound flights, negative for the westbound ones),
be the speed of the plane relative to the (rotating) Earth
(positive for the eastbound flights, negative for the westbound ones),
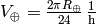 the surface speed of the
Earth, then the proper time for the clocks on the surface is:
the surface speed of the
Earth, then the proper time for the clocks on the surface is:
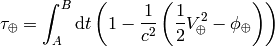
and for the clocks in the plane
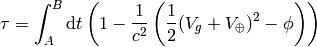
then the difference between the proper times is:
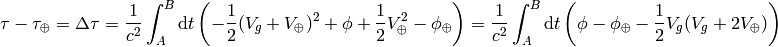
but 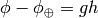 , where
, where 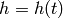 is the altitude of the plane, so
the final formula is:
is the altitude of the plane, so
the final formula is:
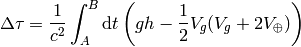
Let’s evaluate it for typical altitudes and speeds of commercial aircrafts:
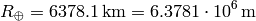
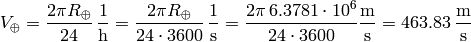
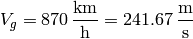
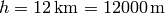
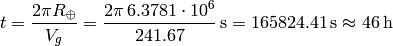
For eastbound flights we get:
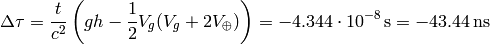
and for westbound flights we get:
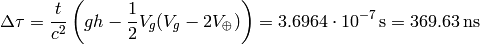
By neglecting gravity, one would get: eastbound flights:
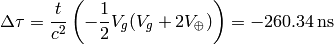
and for westbound flights:
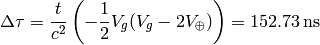
By just taking the clocks to the altitude 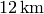 and staying there for 46
hours (without moving with respect to the inertial frame, e.g. far galaxies), one gets:
and staying there for 46
hours (without moving with respect to the inertial frame, e.g. far galaxies), one gets:
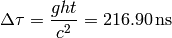
Rotating Disk Metric¶
The rotating disk metrics is (taking weak field gravitation into account):
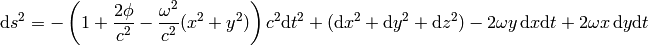
Then:
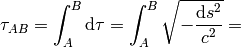
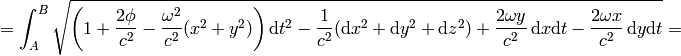
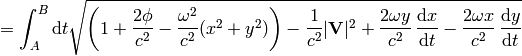
where
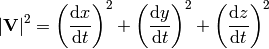
is the nonrelativistic velocity. Then we expand the square root into power
series and only keep terms with low powers of  :
:
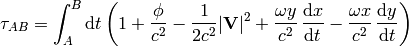
so
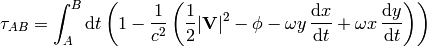
Now as before let 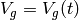 be the speed of the plane (relative to the
rotating Earth, e.g. relative to our frame),
be the speed of the plane (relative to the
rotating Earth, e.g. relative to our frame), 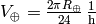 the surface speed of the Earth, so
the surface speed of the Earth, so 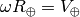 . For the clocks on the surface, we have:
. For the clocks on the surface, we have:
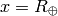
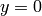
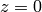
so
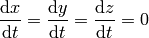
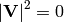
then the proper time for the clocks on the surface is:
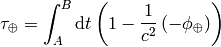
and for the clocks in the plane we have:
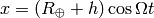
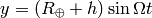
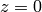
where 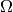 is defined by
is defined by 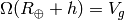 , so
, so
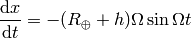
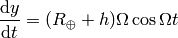
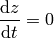
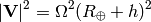
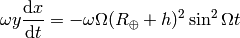
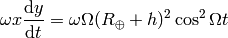
and
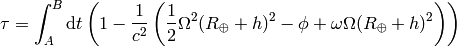
then the difference between the proper times is:
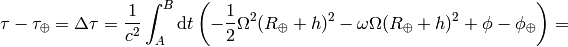
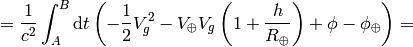
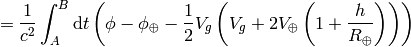
but 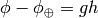 , where
, where 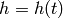 is the altitude of the plane and we
approximate
is the altitude of the plane and we
approximate
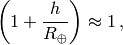
so the final formula is the same as before:
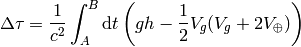
Note: for the values above, the bracket 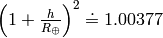 , so it’s effect on the final difference of the
proper times is negligible (e.g. less than
, so it’s effect on the final difference of the
proper times is negligible (e.g. less than 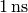 ). The difference is
caused by a slightly vague definition of the speed of the plane, e.g. the
ground speed is a bit different to the speed relative to the rotating Earth
(this depends on how much the atmosphere rotates with the Earth).
). The difference is
caused by a slightly vague definition of the speed of the plane, e.g. the
ground speed is a bit different to the speed relative to the rotating Earth
(this depends on how much the atmosphere rotates with the Earth).
Concluding Remarks¶
The coordinate time 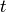 in both cases above is totally different. One can find
some physical clocks in both cases that measure (e.g. whose proper time is) the
particular coordinate time, but the beauty of the differential geometry
approach is that we don’t have to care about this.
in both cases above is totally different. One can find
some physical clocks in both cases that measure (e.g. whose proper time is) the
particular coordinate time, but the beauty of the differential geometry
approach is that we don’t have to care about this. 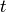 is just a coordinate,
that we use to calculate something physical, like a proper time along some
trajectory, which is a frame invariant quantity. In both cases above, we got a
different formulas for the proper time of the surface clocks (and the clocks in
the plane) in terms of the coordinate time (because the coordinate time is
different in both cases), however the difference of the proper times is the
same in both cases:
is just a coordinate,
that we use to calculate something physical, like a proper time along some
trajectory, which is a frame invariant quantity. In both cases above, we got a
different formulas for the proper time of the surface clocks (and the clocks in
the plane) in terms of the coordinate time (because the coordinate time is
different in both cases), however the difference of the proper times is the
same in both cases:
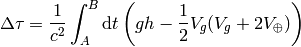
There is still a slight difference though – the 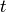 here used to evaluate the
integral is different in both cases. To do it correctly, one should take the
total time as measured by any of the clocks and then use the right formula for
the proper time of the particular clock to convert to the particular coordinate
time. However, the difference is small, of the order of nanoseconds, so it’s
negligible compared to the total flying time of 46 hours.
here used to evaluate the
integral is different in both cases. To do it correctly, one should take the
total time as measured by any of the clocks and then use the right formula for
the proper time of the particular clock to convert to the particular coordinate
time. However, the difference is small, of the order of nanoseconds, so it’s
negligible compared to the total flying time of 46 hours.
FAQ¶
How does one incorporate the fact, that there are only two possible
transformations, into all of this?
For more info, see: http://arxiv.org/abs/0710.3398.
Answer: in that article there are
actually three possible transformations, 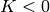 corresponds to O(4),
corresponds to O(4), 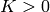 to
O(3, 1) and
to
O(3, 1) and 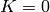 to either of them in the limit
to either of them in the limit 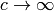 .
.
What is the real difference between the Newtonian physics and special
relativity? E.g. how do we derive the Minkowski metrics, how do we know we
need to set 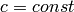 and how do we incorporate gravity in it?
Answer:
there are only three possible groups of transformations: O(4), O(3, 1) and a
limit of either for
and how do we incorporate gravity in it?
Answer:
there are only three possible groups of transformations: O(4), O(3, 1) and a
limit of either for 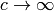 . All three provide inequivalent predictions
for high speeds, so we just choose the right one by experiment. It happens to
be the O(3, 1). As to gravity, that can be incorporated in either of them.
. All three provide inequivalent predictions
for high speeds, so we just choose the right one by experiment. It happens to
be the O(3, 1). As to gravity, that can be incorporated in either of them.
Questions Without Answers (Yet)¶
How can one reformulate the article http://arxiv.org/abs/0710.3398 into the language of the O(4) and O(3, 1) groups above? Basically each assumption and equation must have some counterpart in what we have said above. I’d like to identify those explicitely.
What are all the possible metrics, that generate the Newtonian Christoffel
symbols?
(Several such are given above, but I want to know all of them) Probable answer:
all metrics, whose inverse reduces to 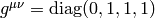 in the
limit
in the
limit 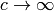 . I would like to have an explicit proof of this though.
. I would like to have an explicit proof of this though.
What is the role of the different metrics, that generate the same Christoffel
symbols in the limit (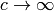 )? Can one inertial frame be given with one
and another frame with a different form of the metrics (e.g. one with
)? Can one inertial frame be given with one
and another frame with a different form of the metrics (e.g. one with
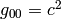 and the other one with
and the other one with 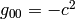 ?) Possible answer: there is
no transformation to convert a metrics with signature +4 to signature +2, so
one has to choose one and then all other inertial frames have the same one.
?) Possible answer: there is
no transformation to convert a metrics with signature +4 to signature +2, so
one has to choose one and then all other inertial frames have the same one.
What are all the allowed transformations between intertial frames? If we assume
that the inertial frames are given with one given metrics (see the previous
question), then the answer is: representation of the O(3, 1) group if
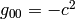 or O(4) group if
or O(4) group if 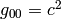 . But if one frame is
. But if one frame is 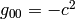 and we transform to another frame with
and we transform to another frame with 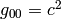 , then it is not clear what
happens. Possible answer: one has to choose some signature and stick to it,
see also the previous question.
, then it is not clear what
happens. Possible answer: one has to choose some signature and stick to it,
see also the previous question.
What is the real difference between Newtonian physics and general relativity? Given our formulation of Newtonian physics using the differential geometry, I want to know what the physical differences are between all the three theories are.