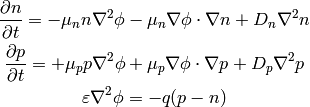Maxwell’s Equations¶
The Maxwell’s equations are:
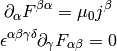
and the Lorentz force is:
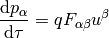
where:
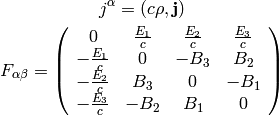
This corresponds to:
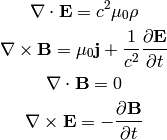
Four Potential¶
The four potential is defined by:
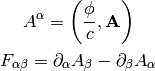
this corresponds to:
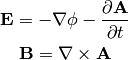
The Maxwell’s equations can then be written as (note that the two eq. without sources are automatically satisfied by the four potential):
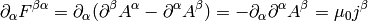
where we have employed the Lorentz gauge 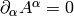 .
.
Semiconductor Device Physics¶
In general, the task is to find the five quantities:
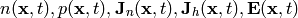
where 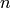 (
(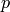 ) is the electron (hole) concentration,
) is the electron (hole) concentration, 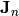 (
(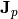 ) is the electron (hole) current density,
) is the electron (hole) current density, 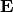 is the
electric field.
is the
electric field.
And we have five equations that relate them. We start with the continuity equation:
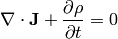
where the current density 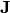 is composed of electron and hole current
densities:
is composed of electron and hole current
densities:
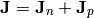
and the charge density 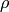 is composed of mobile (electrons and holes) and
fixed charges (ionized donors and acceptors):
is composed of mobile (electrons and holes) and
fixed charges (ionized donors and acceptors):
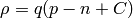
where 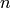 and
and 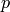 is the electron and hole concetration,
is the electron and hole concetration, 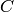 is the net
doping concetration (
is the net
doping concetration (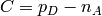 where
where 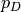 is the concentration of ionized
donors, charged positive, and
is the concentration of ionized
donors, charged positive, and 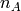 is the concentration of ionized acceptors,
charged negative) and
is the concentration of ionized acceptors,
charged negative) and 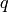 is the electron charge (positive). We get:
is the electron charge (positive). We get:
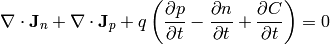
Assuming the fixed charges 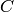 are time invariant, we get:
are time invariant, we get:
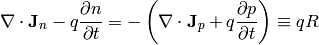
where 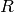 is the net recombination rate for electrons and holes (a positive
value means recombination, a negative value generation of carriers). We get the
carrier continuity equations:
is the net recombination rate for electrons and holes (a positive
value means recombination, a negative value generation of carriers). We get the
carrier continuity equations:
(1)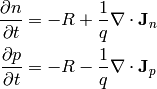
Then we need material relations that express how the current 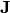 is
generated using
is
generated using 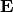 and
and 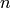 and
and 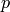 . A drift-diffusion model is to assume
a drift current (
. A drift-diffusion model is to assume
a drift current (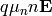 ) and a diffusion (
) and a diffusion (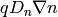 ),
which gives:
),
which gives:
(2)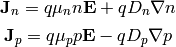
where 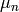 ,
, 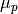 ,
, 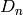 ,
, 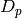 are the carrier mobilities and
diffusivities.
are the carrier mobilities and
diffusivities.
Final equation is the Gauss’s law:
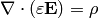
(3)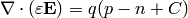
Equations¶
Combining (2) and (1) we get the following three
equations for three unknowns 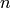 ,
, 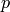 and
and 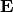 :
:
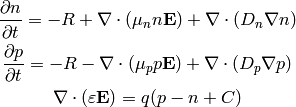
And it is usually assumed that the magnetic field is time independent, so
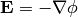 and we get:
and we get:
(4)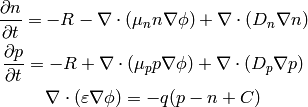
These are three nonlinear (due to the terms 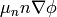 and
and
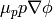 ) equations for three unknown functions
) equations for three unknown functions 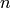 ,
, 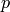 and
and 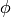 .
.
Example 1¶
We can substract the first two equations and we get:
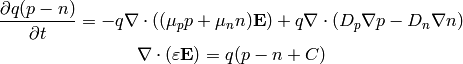
and using 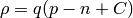 and
and 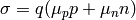 , we get:
, we get:
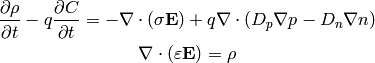
So far we didn’t make any assumptions. Most of the times the net doping
concetration 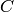 is time independent, which gives:
is time independent, which gives:
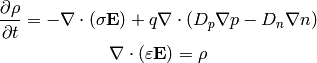
Assuming further 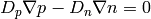 , we just get the equation of
continuity and the Gauss law:
, we just get the equation of
continuity and the Gauss law:
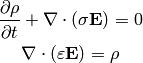
Finally, assuming also that that 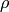 doesn’t depend on
time, we get:
doesn’t depend on
time, we get:
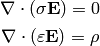
Example 3¶
Let’s calculate the 1D pn-junction. We take the equations (4) and
write them in 1D for the stationary state
(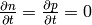 ):
):
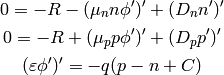
We expand the derivatives and assume that 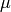 and
and 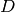 is constant:
is constant:
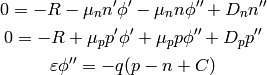
and we put the second derivatives on the left hand side:
(5)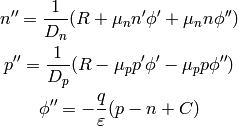
now we introduce the variables 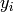 :
:
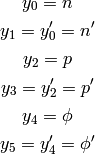
and rewrite (5):
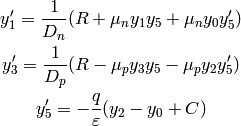
So we are solving the following six nonlinear first order ODE:
(6)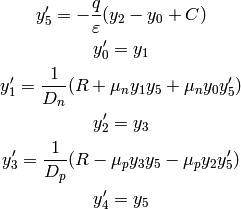
 are position independent and
are position independent and 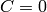 ,
, 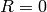 :
: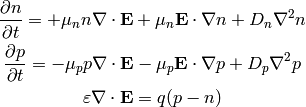
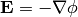 we get:
we get: